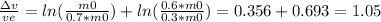Answer:
A)
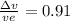
B)

Step-by-step explanation:
Tsiolkovsky rocket equation states that:
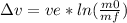
Where
Δv: change of speed of the rocket after burning the fuel
ve: exhaust velocity
m0: initial mass of the rocket
mf: mass of the rorcket after completing the burn (if it burned all its fuel this is the dry mass)
Since the rocket starts from rest (v = 0) its final speed will be the Δv
To express this speed in multiples of the fuel velocity out of the rocket, we simply:
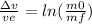
In this case we know that 60% of the mass of the rocket is fuel, so:
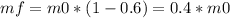
So:

If the rocket jettisons a first stage with 0.3*m0 of fuel, and 0.1*m0 of fuel tank, it will be doing two burns.
The first burn will go from mass m0 to m1
m1 = m0 - 0.3 * m0 = 0.7 * m0
The speed gain from this first burn would be:
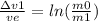
Then it will jettison the tank, since jettisoning is done with small explosives the gain of speed can be ignored for being very small. However it would have lost some mass.
m2 = m1 - 0.1 * m0 = 0.7 * m0 - 0.1 * m0 = 0.6 * m0
Next it will activate the second stage, burning fuel and going from m2 to m3
m3 = m2 - 0.3 * m0 = 0.6 * m0 - 0.3 * m0 = 0.3 * m0
The speed gain of this second burn would be:
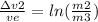
And both added together: