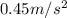Question

Although ungraceful on land, walruses are fine swimmers. They normally swim at 1.94 m/s, and for short periods of time are capable of reaching speeds of nearly 9.72 m/s. Suppose a walrus accelerates from 1.95 m/s to 9.45 m/s over a distance of 95 m. What would be the magnitude of the walrus’s uniform acceleration?

Answer 1

The magnitude of the walrus's uniform acceleration is
`0.45m/s^(2)`

Step-by-step explanation:

First, we need to gather the data the problem provides us with. We know the Walrus will start with a velocity of 1.95 m/s. This will be our initial velocity.

`V_(0)=1.95m/s`

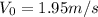
Next, we know that in the end, the walrus will have a velocity of 9.45 m/s, this will be our final velocity.

`V_(f)=9.45m/s`

and finally, we know the walrus will travel 95m before he reaches the final velocity. This will be our displacement.

x= 95m

So we need to look for a formula we can use that contains: initial velocity, final velocity and displacement. Such a formula looks like this:

`a=(V_(f) ^(2)-V_(0) ^(2))/(2x)`

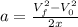
so now we can plug the given data into the formula so we get:

`a=((9.45m/s) ^(2)-(1.95m/s)^(2))/(2(95m))`

`a=(89.3025m^(2)/s^(2) -3.8025m^(2)/s^(2))/(190m)`

`a=(85.5m^(2)/s^(2))/(190m)`

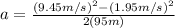
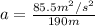
which yields:

a=
`0.45m/s^(2)`

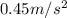
So the magnitude of the walrus's uniform acceleration is
`0.45m/s^(2)`