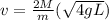Question

A bullet of mass m and speed v passes completely through a pendulum bob of mass M. The bullet emerges with a speed of v/2. The pendulum bob is suspended by a stiff rod of length l and negligible mass. Use conservation of energy and momentum to find the minimum value of v such that the bob will barely swing through a complete vertical circle.

Answer 1

`v = (2M)/(m)(√(4gL))`

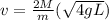
Step-by-step explanation:

After bullet passing through the pendulum we know that the pendulum will raise to its maximum height

So the minimum speed required for this is in such a way that it will reach at highest point with zero speed

so here we can use energy conservation

`(1)/(2)Mv_1^2 = Mg(2L)`

so we will have

`v_1 = √(4gL)`

now we got the speed of the pendulum so we can use now momentum conservation of bullet + pendulum system

here we have

`mv + 0 = Mv_1 + m(v)/(2)`

`mv = M(√(4gL)) + m(v)/(2)`

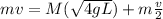
so we have

`m(v)/(2) = M(√(4gL))`

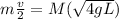
so the speed is given as

`v = (2M)/(m)(√(4gL))`