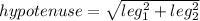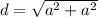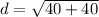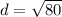Answer:
The correct statements are:
The area of a base is 40 square centimeters.
The area of a lateral side between the bases is about 126.5 square centimeters.
Explanation:
Given information: A right rectangular prism with square bases has Height = 20 cm and volume = 800 cubic cm.
Let a be the length of a side of the base.
Volume of a right rectangular prism is

Volume of prism is


Volume of prism is 800.
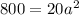
Divide both sides by 20.
 .... (1)
.... (1)
Taking square root both sides.
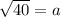
The length of a side of the base is
 centimeters.
centimeters.
Area of square base is
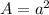
Using (1) we get,
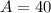
The area of a base is 40 square centimeters.
The area of a lateral side between the bases is
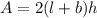
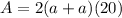
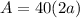
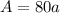
Substitute the value of a.
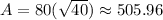
Therefore the area of a lateral side between the bases is about 505.96 square centimeters.
The area of a lateral side is

Diagonals of base: Using Pythagoras we get