Answer:
Third option: The graph moves left 18 units.
Explanation:
Some transformations for a function f(x) are shown below:
If
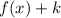 , the function is shifted up "k" units.
, the function is shifted up "k" units.
If
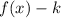 , the function is shifted down "k" units.
, the function is shifted down "k" units.
If
 , the function is shifted left "k" units.
, the function is shifted left "k" units.
If
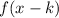 , the function is shifted right "k" units.
, the function is shifted right "k" units.
In this case, we can observe that graph of
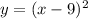 is changed to
is changed to
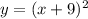
Since:

We can conclude that the function
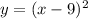 is shifted left 18 units to get the function
is shifted left 18 units to get the function
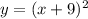 .
.