Question

Use induction to show that 12 + 22 + 32 + ... + n2 = n(n+1)(2n+1)/6, for all n > 1.

Answer 1

Answer with Step-by-step explanation:

Let
`P(n)=1^2+2^2+3^2+.....+n^2=(n(n+1)(2n+1))/(6)`

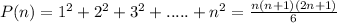
Substitute n=2

Then
`P(2)=1+2^2=5`

`P(2)=(2(2+1)(4+1))/(6)=5`

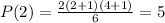
Hence, P(n) is true for n=2

Suppose that P(n) is true for n=k >1

`P(k)=1^2+2^2+3^2+...+k^2=(k(k+1)(2k+1))/(6)`

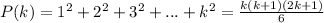
Now, we shall prove that p(n) is true for n=k+1

`P(k+1)=1^2+2^2+3^2+...+k^2+(k+1)^2=((k+1)(k+2)(2k+3))/(6)`

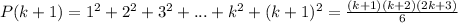
LHS

`P(k+1)=1^2+2^2+3^2+.....+k^2+(k+1)^2`

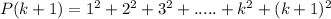
Substitute the value of P(k)

`P(k+)=(k(k+1)(2k+1))/(6)+(k+1)^2`

`P(k+1)=(k+1)((k(2k+1)/(6))+k+1)`

`P(k+1)=(k+1)((2k^2+k+6k+6)/(6))`

`P(k+1)=(k+1)((2k^2+7k+6)/(6))`

`P(k+1)=(k+1)((2k^2+4k+3k+6)/(6))`

`P(k+1)=((k+1)(k+2)(2k+3))/(6)`

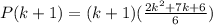
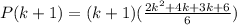
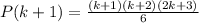
LHS=RHS

Hence, P(n) is true for all n >1.

Hence, proved