Answer:

Explanation:
We have the grid has m horizontal lines and n vertical lines
We have to find the number of rectangles
If the grid is 1×1, there is 1 rectangle.
If the grid is 2×1, there will be 2 + 1 = 3 rectangles
If it grid is 3×1, there will be 3 + 2 + 1 = 6 rectangles.
So is there is
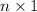 there will be
there will be
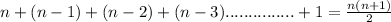
If we add one column to
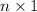 firstly we will have as many rectangles in the 2nd column as the first,
firstly we will have as many rectangles in the 2nd column as the first,
And then we have that same number of
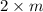 rectangles.
rectangles.
So for
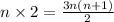 rectanglesAfter solving this we can say
rectanglesAfter solving this we can say
For
 we have
we have
 rectangles.
rectangles.