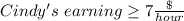Question

Peter works part time for 3 hours every day and Cindy works part time for 2 hours every day.

A. If both of them get $4.50 an hour, write an inequality to compare Peter's and Cindy's earnings.

B. What should Cindy's per-hour income be so that she earns at least $14 a day? Write an inequality and explanation of how to solve it.​

Answer 1

A) 13.50>9.00

B) $7

Explanation:

A) 4.50*3=13.50 (Peter) 4.50*2=9.00 (Cindy)

B) Cindy would have to earn $7 an hour if she works 2 hours per day because 7*2=14

Answer 2

Givens:

• Peter 3 hours every day.
• Cindy works 2 hours every day.
• Each of them get $4.50 per hour.

So, from the problem we can deduct that Peter earns $4.50(3 hours/day) = $13.50 per day. And Cindy earns $4.50(2 hours/day) = $9.00 per day. Therefore, Peter daily earning are higher than Cindy's, this can be expressed with the following inequality:

Peter's daily earnings > Cindy's daily earnings

$13.50 > $9.00

On the other hand, if Cindy earns at least $14 per day, that means she earns $14/2 hours per day = $7 per hour, because she only works 2 hours each day. But, the problem says "at least", so the correct expression would be

`Cindy's \ earning \geq 7 (\$)/(hour)`