Question

Light enters an equilateral prism with an incident angle of 35° to the normal of the surface. Calculate the angle at which the light exits on the opposite side. The index of refraction of the glass is 1.50.

Answer 1

65.9°

Step-by-step explanation:

When light goes through air to glass

angle of incidence, i = 35°

refractive index, n = 1.5

Let r be the angle of refraction

Use Snell's law

`n=(Sini)/(Sinr)`

`1.5=(Sin35)/(Sinr)`

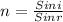
Sin r = 0.382

r = 22.5°

Now the ray is incident on the glass surface.

A = r + r'

Where, r' be the angle of incidence at other surface

r' = 60° - 22.5° = 37.5°

Now use Snell's law at other surface

`(1)/(n)=(Sinr')/(Sini')`

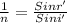
Where, i' be the angle at which the light exit from other surface.

`(1)/(1.5)=(Sin37.5')/(Sini')`

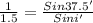
Sin i' = 0.913

i' = 65.9°