Answer:
No, function is not one-to-one
No, function is not onto
Explanation:
We are given that a function
f:
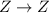
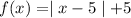
If function is one-to-one then different x have different image .
Domain =Z
Codomain=Z
When function is onto then range=Codomain
Substitute x=1
Then ,
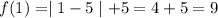
When substitute x=9
Then , we get
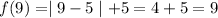
Image of 1 and 9 are same hence, function is not one-to-one.
Negative elements of Z and Zero has no preimage.Therefore, function is not onto.