Question

4. Let B = {(1,0,1),(0,1,2), (2, -1,0)}. (a) The vectors in B are dependent. Show this. (b) Find a non-trivial solution to an(1,0,1) + a2(0,1,2) + a3(2, -1,0) = 0. (c) B is not a basis for the span(B). Find a basis for the span span(B).

Answer 1

Explanation:

Given are three vectors in set B.

To show that B is dependent

The determinant

`\left[\begin{array}{ccc}1&0&1\\0&1&2\\2&-1&0\end{array}\right] \\=1(2)-1(2) =0`

Hence vectors are dependent

b) The given equation
`a_1(1,0,1) + a_2(0,1,2) + a_3(2, -1,0) = 0.\\`

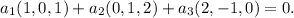
Let us try parametrically

These 3 vectors are collinear and hence equation would be

`(x-1)/(0-1) =(y-0)/(1) =(z-1)/(2-1) =s\\(x,y,z) = (1-s, s, 1+s)`

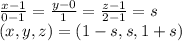
c) Basis for B would be only 2 dimensional

i.e. any two vectors out of 3 form basis

The basis would be (1,0,1) and (0,1,2)