Question

Triangle ABC with vertices A(2, 4) , B(4, 0) , and C(6, 6) is dilated about the origin to be triangle A′B′C′ .

Answer 1

Triangle ABC is dilated by a scale factor of 1.5

Explanation:

Givens

• The vertices of the original triangle are A(2,4), B(4,0) and C(6,6).

According to the graph, the vertices of the dilated triangle are A'(3,6), B'(6,0) and C'(9,9).

Notice that the dilation factor is a quotient between a dilated coordinate and an original coordinate. If we do this division

`(3)/(2)=1.5\\(6)/(4)=1.5\\ (9)/(6)=1.5`

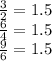
Therefore, the dilation factor is 1.5.

The right answer is the second choice.

Answer 2

Triangle ABC is dilated by a scale factor of 1.5

Explanation:

The general rule for the dilation about the origin with a factor of k is

`(x,y)\rightarrow (kx,ky)`

You are given two triangles ABC and A'B'C'.

In triangle ABC:

• A(2,4)
• B(4,0)
• C(6,6)

From the diagram, in triangle A'B'C':

• A'(3,6)
• B'(6,0)
• C'(9,9)

As you can see

• 
  `A(2,4)\rightarrow A'\left((3)/(2)\cdot 2,\ (3)/(2)\cdot 4\right)=A'(3,6)`
• 
  `B(4,0)\rightarrow B'\left((3)/(2)\cdot 4,\ (3)/(2)\cdot 0\right)=B'(6,0)`
• 
  `C(6,6)\rightarrow C'\left((3)/(2)\cdot 6,\ (3)/(2)\cdot 6\right)=C'(9,9)`

So, triangle ABC is dilated by a scale factor of
`(3)/(2)=1.5`