Question

A proton and an electron are both accelerated to the same final speed. If λp s the de Broglie wavelength of the proton and e is the de Broglie wavelength of the electron, then 5, D) Not enough data to answer this question

Answer 1

Step-by-step explanation:

The relation between the de Broglie wavelength and the momentum of the particle is given by

`\lambda =(h)/(m* v)`

where, m is the mas of the particle and v be the velocity of the particle and h be the Plank's constant.

So, the de broglie wavelength of proton is given by

`\lambda _(p)=(h)/(m_(p)* v)` .... (1)

The de broglie wavelength of electron is given by

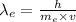`\lambda _(e)=(h)/(m_(e)* v)` .... (2)

Divide equation (2) by equation (1), we get

`(\lambda _(e))/(\lambda _(p))=(m_(p))/(m_(e))`

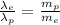
As the mass of proton is much more than the mass of electron, so the de broglie wavelength of electron is more than the de Broglie wavelength of proton.