Question

A ray of light in air is incident at an angle of 25.0° on a glass slide with index of refraction 1.51. (a) At what angle is the ray refracted? ________° from the normal (b) If the wavelength of the light in vacuum is 580 nm, find its wavelength in the glass. ________ nm

Answer 1

16.25° , 348.11 nm

Step-by-step explanation:

Using Snell's law as:

`n_i* {sin\theta_i}={n_r}*{sin\theta_r}`

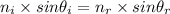
Where,

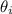`{\theta_i}` is the angle of incidence ( 25.0° )

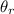`{\theta_r}` is the angle of refraction ( ? )

`{n_r}` is the refractive index of the refraction medium (glass, n=1.51)

`{n_i}` is the refractive index of the incidence medium (air, n=1)

Hence,

`1* {sin25.0^0}={1.51}*{sin\theta_r}`

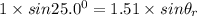
Angle of refraction =
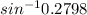`sin^(-1)0.2798` = 16.25°

Refractive index is equal to velocity of the light 'c' in empty space divided by the velocity 'v' in the substance.

Or ,

n = c/v.

The frequency of the light does not change but the wavelength of the light changes with change in the speed.

c = frequency × Wavelength

Frequency is constant,

The formula can be written as:

n = λ / λn.

Where,

λn is the wavelength in the medium

λ is the wavelength in vacuum (580 nm)

So,

1.51 = 580 / λn

λn = 348.11 nm