Question

A ballistic pendulum is a device used to measure the speed of a bullet. A bullet is fired at a block of wood hanging from two strings. The bullet embeds itself in the block and causes the combined block plus bullet system to swing up. If the bullet is fired at 530 m/s and its mass is 6.5 g, what is the speed of the block and the embedded bullet after collision? The mass of the block is 2.2 kg.

Using the same data from question 8, and the answer to question 8, how high will the pendulum’s block and the embedded bullet rise?

Answer 1

1.56 m/s, 0.124 m

Step-by-step explanation:

mass of bullet, m = 6.5 g = 0.0065 kg

initial velocity of bullet, u = 530 m/s

mass of block, M = 2.2 kg

initial velocity of block, v = 0 m/s

Let the speed of bullet and block system after the collision is V.

By use of conservation of momentum

Momentum of system before collision = Momentum of system after collision

Momentum of bullet before collision + momentum of block before collision = Momentum of (bullet + block) after collision

m x u + M x v = (M + m) x V

0.0065 x 530 + 0 = (2.2 + 0.0065) x V

3.445 = 2.2065 x V

V = 1.56 m / s

Thus, the velocity of bullet and block system after collision is 1.56 m/s.

Now use the conservation of energy

The kinetic energy at the bottom is equal to the potential energy at the height.

Let the height raised is h.

`(1)/(2)(M+m)V^(2)=(M+m)gh`

`(1)/(2)* 1.56 * 1.56=9.8* h`

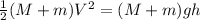
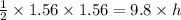
h = 0.124 m

Thus, the height raised is 0.124 m.