Question

A rectangle has a height of c^3+6c^2+2c and a width of c^2+1

Express the area of the entire rectangle.

Your answer should be a polynomial in standard form.

Area=

Answer 1

`A = c^5+6c^4+3c^3+6c^2+2c`

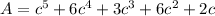
Explanation:

The dimensions of a rectangle are length and breadth/width

Here we are given height . Assuming it to be one of the side of the rectangle , we will do the further calculation

Hence one side is

side 1 =
`c^2+1`

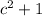
And the other side is

Side 2 =
`c^3+6c^2+2c`

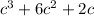
The area of rectangle = side 1 x side 2

`A= (c^2+1) * (c^3+6c^2+2c)`

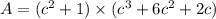
Distributing parenthesis

`=c^2c^3+c^2\cdot \:6c^2+c^2\cdot \:2c+1\cdot \:c^3+1\cdot \:6c^2+1\cdot \:2c`

`=c^3c^2+6c^2c^2+2c^2c+1\cdot \:c^3+1\cdot \:6c^2+1\cdot \:2c`

`=c^5+6c^4+2c^3+c^3+6c^2+2c`

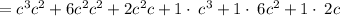
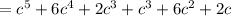
adding similar terms

`c^5+6c^4+3c^3+6c^2+2c`

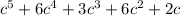
Hence Area is given by the above polynomial