Answer:
He should stand from the center of laser pointed on the wall at 1.3 m.
Step-by-step explanation:
Given that,
Wave length = 650 nm
Distance =10 m
Double slit separation d = 5 μm
We need to find the position of fringe
Using formula of distance
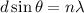
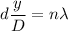
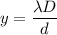
Put the value into the formula
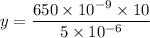
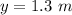
Hence, He should stand from the center of laser pointed on the wall at 1.3 m.