Question

Mustard gas, used in chemical warfare in World War I, has been found to be an effective agent in the chemotherapy of Hodgkin's disease. It can be produced according to the following reaction: SCl (g)+ 2C H, (g)S(CH2CH2CI)2 (g) An evacuated 5.0 L flask at 20.0°C is filled with 0.258 mol SC12 and 0.592 mol C2H4. After equilibrium is established, 0.0349 mol mustard gas is present. (a) What is the partial pressure of each gas at equilibrium? (b) What is K at 20.0°C?

Answer 1

Step-by-step explanation:

(a) The given reaction equation is as follows.

`SCl_(2)(g) + 2C_(2)H_(4)(g) \rightleftharpoons S(CH_(2)CH_(2)Cl)_(2)(g)`

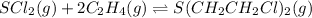
The given data is as follows.

Volume of the flask (V) = 5.0 L

Temperature (T) = (20.0^{o}C + 273.15) = 293.15 K

Number of moles of
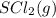`SCl_(2)(g)` = 0.258 mol

Number of moles of
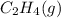`C_(2)H_(4)(g)` = 0.592 mol

Number of moles of
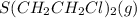`S(CH_(2)CH_(2)Cl)_(2)(g)` at equilibrium = 0.0349 mol

Hence, calculate the partial pressures of each given quantity using the ideal gas law formula as follows.

PV = nRT

or, P =
`(nRT)/(V)`

`P_{SCl_(2)` =
`(0.258 mol * 0.08206 L.atm/mol.K * 293.15 K)/(5.0 L)`

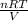
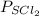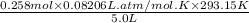
= 1.24 atm

Similarly,

`P_{C_(2)H_(4)` =
`(0.592 mol * 0.08206 L.atm/mol.K * 293.15 K)/(5.0 L)`

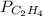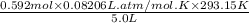
= 2.848 atm

Also,

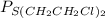`P_{S(CH_(2)CH_(2)Cl)_(2)`(equiiibrium) =
`(0.0349 mol * 0.08206 L.atm/mol.K * 293.15 K)/(5.0 L)`

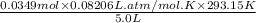
= 0.168 atm

For the reaction,
`SCl_(2)(g) + 2C_(2)H_(4)(g) \rightleftharpoons S(CH_(2)CH_(2)Cl)_(2)(g)`

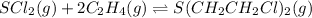
Initial : 1.241 2.848 0

Change : -x -2x +x

Equilibrium : (1.241 - x) (2.848 - 2x) x

Therefore, calculate partial pressure of each gas at equilibrium as follows.

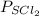`P_{SCl_(2)` = 1.241 - x

= (1.241 - 0.168)

= 1.073 atm

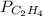`P_{C_(2)H_(4)` = 2.848 - 2x

=
`(2.848 - 2 * 0.168)`

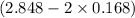
= 2.512 atm

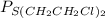`P_{S(CH_(2)CH_(2)Cl)_(2)` = x = 0.168 atm

(b) The equilibrium constant for the reaction will be as follows.

`K_(p)` =
`\frac{P_{S(CH_(2)CH_(2)Cl)_(2)}}{P_{SCl_(2)} * P^(2)_{C_(2)H_(4)}}`

=
`(0.168)/(1.073 * (2.512)^(2))`

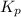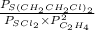
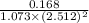
= 0.0248

= 0.025 (approx)

Therefore, K at
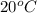`20^(o)C` is 0.025 (approx).