Answer:
The number of positive divisors are 7.
Explanation:
Since it is given that p and q are prime numbers thus they will not have any divisors other that itself and 1
The number
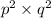 can be represented as
can be represented as
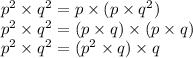
Thus the number
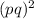 can be divided by:
can be divided by:
1)

2)
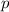
3)
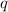
4)
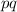
5)
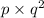
6)
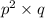
7)
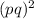
Thus the number of positive divisors are 7.