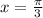Answer:
Amplitude = 2; period = two times pi over three; phase shift: x equals pi over three
Explanation:
The given function is
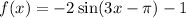
Comparing to
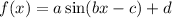 , we have a=-2 , b=3,
, we have a=-2 , b=3,
 and d=-1.
and d=-1.
The amplitude is
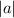 .
.
This implies that amplitude is

The period is
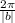
This implies period is
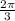
The phase shift is
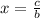
This implies that phase shift is