Answer:
The kinetic energy and speed of the two helium atoms are
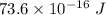 and
and
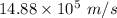 .
.
Step-by-step explanation:
Given that,
Mass of beryllium = 8.00 u
Mass of helium = 4.00 u
Energy = 92.2 keV
We need to calculate the kinetic energy
The kinetic energy of the helium atom is the half of the total kinetic energy released.

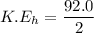
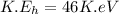
Therefore, the kinetic energy of the each helium atom is

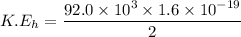

We need to calculate the speed
Using formula of speed
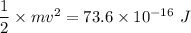
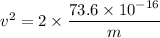
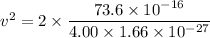

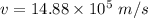
Hence, The kinetic energy and speed of the two helium atoms are
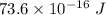 and
and
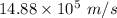 .
.