Question

A horizontal string is attached at one end to an electrical vibrator of frequency 50.0 Hz, and at the other to a set of hanging masses. The string has a mass per unit length 0.115 gm^-1. When the string has a length 210.4 cm five loops are observed. What mass (in grams) is hung from the string? You adjust the frequency so that you now observe 4 loops on the string leaving the hanging mass and string length the same. What is the new frequency?

Answer 1

The mass of the string and new frequency are 20.78 g and 40.0 Hz.

Step-by-step explanation:

Given that,

Frequency = 50.0 Hz

Mass per unit length = 0.115 g/m

String length = 210.4 cm

Number of loops = 5

We need to calculate the mass is hung from the string

Using formula of frequency

`f=(5)/(2L)\sqrt{(T)/(M)}`

`f=(5)/(2L)\sqrt{(mg)/(M)}`

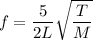
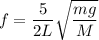
Where, f = frequency

M = mass per unit length

T = tension

Put the value into the formula

`50.0=(5)/(2*210.4)\sqrt{(m*9.8)/(0.115)}`

`m=(50^2*((2*210.4*10^(-2))/(5))^2*0.115*10^(-3))/(9.8)`

`m=0.02078\ kg`

`m=20.78\ g`

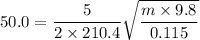
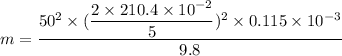
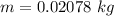
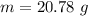
We need to calculate the new frequency for 4 loops

Using formula of frequency

`f=(4)/(2*210.4*10^(-2))\sqrt{(0.02078*9.8)/(0.115*10^(-3))}`

`f=40.0\ Hz`

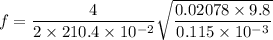
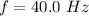
Hence, The mass of the string and new frequency are 20.78 g and 40.0 Hz.