Question

In young’s double slit experiment, the measured fringe width is 0.5 mm for a Sodium light of 589 nm at a distance of 1.5 m. A bright fringe is at a distance of 1 cm from the center.

A) Find the order of the bright fringe
B) Calculate the width of the bright fringe

Answer 1

(A). The order of the bright fringe is 6.

(B). The width of the bright fringe is 3.33 μm.

Step-by-step explanation:

Given that,

Fringe width d = 0.5 mm

Wavelength = 589 nm

Distance of screen and slit D = 1.5 m

Distance of bright fringe y = 1 cm

(A) We need to calculate the order of the bright fringe

Using formula of wavelength

`\lambda=(dy)/(mD)`

`m=(d y)/(\lambda D)`

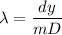
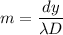
Put the value into the formula

`m=(1*10^(-2)*0.5*10^(-3))/(589*10^(-9)*1.5)`

`m=5.65 = 6`

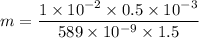
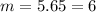
(B). We need to calculate the width of the bright fringe

Using formula of width of fringe

`\beta=(yd)/(D)`

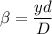
Put the value in to the formula

`\beta=(1*10^(-2)*0.5*10^(-3))/(1.5)`

`\beta=3.33*10^(-6)\ m`

`\beta=3.33\ \mu m`

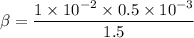
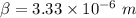
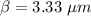
Hence, (A). The order of the bright fringe is 6.

(B). The width of the bright fringe is 3.33 μm.