Question

The exhaust nozzle of a jet engine expands air at 300 kPa and 180°C adiabatically to 100 kPa. Determine: (a) The air velocity at the exit when the inlet velocity is low, and (b) The nozzle isentropic efficiency is 96 percent.

Answer 1

air velocity at the exit, v' = 15.3 m/s

Given:

Temperature, T =
`180^(\circ) = 273 + 180^(\circ) = 453 K`

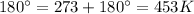
Pressure, P = 300 kPa

Pressure, P' = 100 kPa

isentropic efficiency,
`\eta_(s) = 96%`

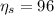
Solution:

In case of isentropic process:

`(T_(s))/(T) = ((P')/(P))^{(k - 1)/(k)}`

`{T_(s) = 453* ((100)/(300))^{(1.4 - 1)/(1.4)}`

`{T_(s) = 453* 0.0233 = 330.96 K`

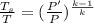
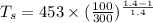
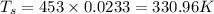
Using steady flow energy eqn:

`h + (v^(2))/(2) = h' + (v'^(2))/(2)`

`h - h' = (v'^(2))/(2) - (v^(2))/(2)`

`mC_(p)(T - T') = (1)/(2)m(v'^(2) - v^(2))`

`C_(p)(T - T') = (1)/(2)(v'^(2) - v^(2))`

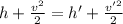
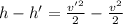
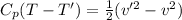
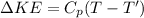`\Delta KE = C_(p)(T - T')` (1)

Now, by using eqn (1), we can calculate the isentropic kinetic energy:

`\Delta KE = C_(p)(T - T_(s))`

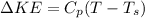
where

`C_(p) = 1.005 kJ/kgK`

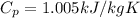
Now,

`\Delta KE = 1.005* (453 - 330.96) = 122.04 kJ/kg`

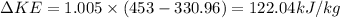
(a) For actual kinetic energy :

`\eta_(s) = (\Delta KE_(actual))/(\Delta KE)`

`0.96 = (\Delta KE_(actual))/(122.04)`

`\Delta KE_(actual) = 117.16 kJ/kg`

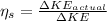
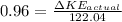
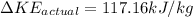
Also,

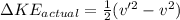`\Delta KE_(actual) = (1)/(2)(v'^(2) - v^(2))` (2)

Now,

(a) air velocity at the exit, v = 0:

Using eqn (2):

`117.16 = (1)/(2)(v'^(2))`

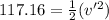
v' = 15.3 m/s