Question

A 10-mm drill rod was heat-treated and ground. The measured hardness He was found to be 300 Brinell. Estimate the endurance strength S. in MPa if the rod is used in rotating bending

Answer 1

The endurance strength for the rod is 434.6 MPa

Step-by-step explanation:

Since the rod is used in rotating bending, we need to use Marin equation given by

`S=k_ak_bS'_e`

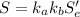
Here S stands for the endurance strength for rotating bending,
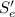`S'_e` is the endurance strength, and
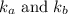`k_a \text{ and } k_b` are the parameters for Marin surface modification factor.

Endurance strength.

We can start finding the endurance strength, from the directions we know that the hardness
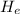`H_e` was found to be 300 Brinell, thus for such value we can find the ultimate tensile strength using

`S_(ut)=3.41H_e`

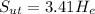
Replacing the hardness we get

`S_(ut)=3.41(300) MPa \\ S_(ut)=1023 MPa`

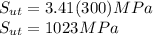
Now since the ultimate tensile strength has a value less than 1400 MPa, we can find the endurance strength using

`S'_e =0.5S_(ut)`

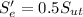
Replacing the tensile strength we get

`S'_e=0.5(1023) MPa \\ S'_e = 511.5 MPa`

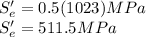
Parameters for Marin surface modification factor.

From the directions we know that the drill rod has a ground surface finish, so then from tables we get

`a=1.58 \text{ and } b = -0.085`

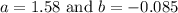
Thus the surface factor will be

`k_a=a(S_(ut))^b`

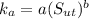
Replacing values and the ultimate tensile strength

`k_a=(1.58)1023^(-0.085)\\k_a=0.8766`

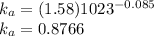
Then we can find the rotating shaft factor, for a diameter of 10 mm, we can use the equation

`k_b=1.24d^(-0.107)`

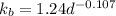
Replacing the diameter we get

`k_b=1.24(10)^(-0.107)\\k_b=0.9692`

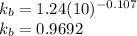
Estimating endurance strength for rotating shaft.

We can replace now all values we have found in Marin equation.

`S=k_ak_bS'_e`

`S=(0.8766)(0.9692)(511.5) MPa`

`S=434.6 MPa`

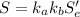
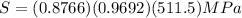
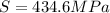
Thus the endurance strength for the rod is 434.6 MPa