Question

A software company uses two quality assurance (QA) checkers X and Y to check an application for bugs. X misses 11% of the bugs and Y misses 13%. Assume that the QA checkers work independently.

(a) What is the probability (as a %) that a randomly chosen bug will be missed by both QA checkers

(b) If the program contains 1,000 bugs, what number of bugs can be expected to be missed? (Round your answer to the nearest integer.)

Answer 1

Given : X misses 11% of the bugs and Y misses 13%.

To Find : a)What is the probability (as a %) that a randomly chosen bug will be missed by both QA checkers

b)If the program contains 1,000 bugs, what number of bugs can be expected to be missed?

Solution:

Probability of missing bugs by QA X = 11% = 0.11

Probability of missing bugs by QA Y = 13% = 0.13

So,the probability that a randomly chosen bug will be missed by both QA checkers =
`0.11 * 0.13= 0.0143 =1.43\%`

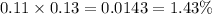
Now we are given that there are 1000 bugs

No. of Bugs can be expected to be missed =
`0.0143 *  1000`

=
`14.3`

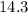
So, 15 bugs can be expected to be missed