Question

A charge of 7.00 mC is placed at opposite corners corner of a square 0.100 m on a side and a charge of -7.00 mC is placed at other opposite corners. Determine the magnitude and direction of the force on right lower corner. Please explain.

Answer 1

4.03\times10^{7}N[/tex], 135°

Step-by-step explanation:

charge, q = 7 mC = 0.007 C

charge, - q = - 7 mC = - 0.007 C

d = 0.1 m

Let the force on charge placed at C due to charge placed at D is FD.

`F_(D)=(kq^(2))/(DC^(2))`

`F_(D)=(9 *10^(9)* 0.007 * 0.007)/(0.1^(2))=4.41 * 10^(7)N`

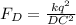
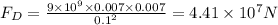
The direction of FD is along C to D.

Let the force on charge placed at C due to charge placed at B is FB.

`F_(B)=(kq^(2))/(BC^(2))`

`F_(B)=(9 *10^(9)* 0.007 * 0.007)/(0.1^(2))=4.41 * 10^(7)N`

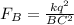
The direction of FB is along C to B.

Let the force on charge placed at C due to charge placed at A is FA.

`F_(A)=(kq^(2))/(AC^(2))`

`F_(D)=(9 *10^(9)* 0.007 * 0.007)/(0.1 *√(2) * 0.1 *√(2))=2.205 * 10^(7)N`

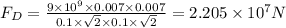
The direction of FA is along A to C.

The net force along +X axis

`F_(x)=F_(A)Cos45-F_(D)`

`F_(x)=2.205*10^(7)Cos45-4.41*10^(7)=-2.85*10^(7)N`

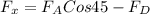
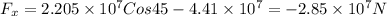
The net force along +Y axis

`F_(y)=F_(B)-F_(A)Sin45`

`F_(y)=4.41*10^(7)-2.205*10^(7)Sin45=2.85*10^(7)N`

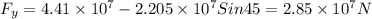
The resultant force is given by

`F=\sqrt{F_(x)^(2)+F_(y)^(2)}=\sqrt{(-2.85*10^(7))^(2)+(2.85*10^(7))^(2)}`

`F = 4.03*10^(7)N`

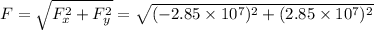
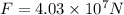
The angle from x axis is Ф

tan Ф = - 1

Ф = -45°

Angle from + X axis is 180° - 45° = 135°