Answer with Step-by-step explanation:
We are given that a set of polynomials
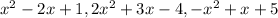
We have to find that given set is a linearly independent set in

and given set is a basis for
 or not.
or not.
Matrix of given set of polynomials
A=
![\left[\begin{array}{ccc}1&-2&1\\2&3&-4\\-1&1&5\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/xo9xjejv73fxkhy0v1kgtyz9v71luc2tey.png)
Linearly Independent set :If any row or any column is not a linear combination of other rows or columns then the set is linearly independent set.
Any row or column is not a linear combination of other rows or columns.Therefore, given set is a linearly independent set .
We know that
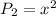
Element of
 is of the form
is of the form

Every element of
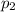 is a linear combination of given set of polynomials.
is a linear combination of given set of polynomials.
Hence, given set is linearly independent in
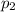 .
.
If any set is basis for any vector space then it satisfied the following two conditions
1.Given set is linearly independent.
2.Every element of given vector space spanned by the given set.
Given set of polynomials are linearly independent and spanned every element of
 .
.
Therefore, given set is as basis for
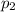 because the set is linearly independent and spanned
because the set is linearly independent and spanned
 .
.