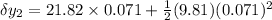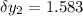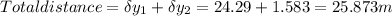Question

A tuning fork vibrating at 509 Hz falls from rest and accelerates at 9.80 m/s^2. How far below the point of release is the tuning fork when waves of frequency of 486 Hz reach the release point? (Take the speed of sound in air to be 343 m/s.). I need answer in meters. Thanks.

Answer 1

Answer:25.873 m

Step-by-step explanation:

Original frequency
`(f_s)=509 Hz`

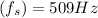
Acceleration due to gravity =9.80 m/s^2

Observed frequency
`(f_0) =486 Hz`

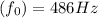
When the source is receding from stationary observer then

`f_0=f_s\left [ (v)/(v-(-v_s)) \right ]`

`f_0=f_s\left [ (v)/(v+v_s) \right ]`

`v_s=v\left [ (f_s)/(f_0)-1\right ]`

`v_s=340\left [(514)/(483)-1 \right ]`

`v_s=21.82 m/s`

`velocity =(distance)/(tme)`

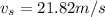
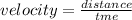
Distance tuning fork has fallen to reach this speed

`\delta y=(v^2-0)/(2a)`

`\delta y=((21.82)^2)/(2* 9.8)`

`\delta y=24.29 m`

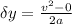
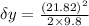
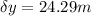
Time required to reach the sound to the observer

`t=(\delta y_1)/(v)`

`t=(24.29)/(340)`

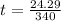
t=0.071 s

During this time fork has traveled an additional distance of

`\delta y_2=v_st+(1)/(2)at^2`

`\delta y_2=21.82* 0.071+(1)/(2)(9.81)(0.071)^2`

`\delta y_2=1.583`

`Total distance=\delta y_1+\delta y_2=24.29+1.583=25.873 m`