A 6cm OD, 2cm thick copper hollow sphere [k=386W/m.C] is uniformly heated at the inner surface at a rate of 150W/m2. The outside surface is cooled with air at 20C with a heat tr…

Question

asked Feb 2, 2020 113k views

1 Answer

Borisbn · Answer 1 · 2020-02-06T18:01:07+0000

Answer:

The outside surface temperature=21.66 C.

Step-by-step explanation:

Given that

Outer diameter=6 cm

Inner diameter=2 cm

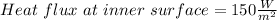
$Heat\ flux\ at\ inner\ surface\q=150(W)/(m^2)$

Outside temperature=20 C

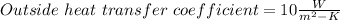
$Outside\ heat\ transfer\ coefficient=10(W)/(m^2-K)$

To find the outside temperature

Heat out from sphere=Heat absorb by surrounding

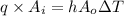
$q* A_i=hA_o\Delta T$

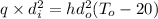
q* d_i^2=hd_o^2(T_o-20)

Now by putting the values

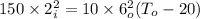
150* 2_i^2=10* 6_o^2(T_o-20)

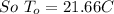
$So\ T_o=21.66C$

So the outside surface temperature=21.66 C.