Question

A 30.0-μF capacitor is connected to a 49.0-Ω resistor and a generator whose rms output is 30.0 V at 60.0 Hz. (a) Find the rms current in the circuit(A)

(b) Find the rms voltage drop across the resistor(V)
(c) Find the rms voltage drop across the capacitor(V)

Answer 1

Step-by-step explanation:

Given that,

Capacitor = 30μC

Resistor = 49.0Ω

Voltage = 30.0 V

Frequency = 60.0 Hz

We need to calculate the impedance

Using formula of impedance

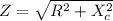`Z=\sqrt{R^2+X_(c)^2}`.....(I)

We need to calculate the value of
`X_(c)`

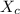
Using formula of
`X_(c)`

`X_(c)=(1)/(2\pi f c)`

`X_(c)=(1)/(2*\pi*60.0*30*10^(-6))`

`X_(c)=88.42\ \Omega`

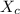
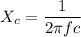
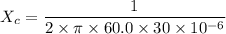
Put the value of
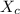`X_(c)` into the formula of impedance

`Z=√((49.0)^2+(88.42)^2)`

`Z=101.08\ \Omega`

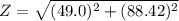
(a). We need to calculate the rms current in the circuit

Using formula of rms current

`I_(rms)=(V)/(Z)`

`I_(rms)=(30.0)/(101.08)`

`I_(rms)=0.30\ A`

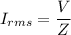
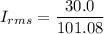
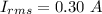
The rms current in the circuit is 0.30 A.

(b). We need to calculate the rms voltage drop across the resistor

Using formula of rms voltage

`V_(rms)=I_(rms)* R`

Put the value into the formula

`V_(rms)=0.30*49.0`

`V_(rms)=14.7\ V`

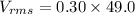
The rms voltage drop across the resistor is 14.7 V

(c). We need to calculate the rms voltage drop across the capacitor

Using formula of rms voltage

`V_(rms)=I_(rms)* X_(C)`

`V_(rms)=0.30*88.42`

`V_(rms)=26.53\ V`

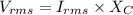
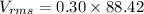
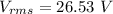
The rms voltage drop across the capacitor is 26.53 V.

Hence, This is the required solution.