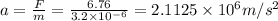Answer:
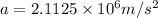
θ = 65.9°
Step-by-step explanation:
mass of the body, m = 3.2 x 10^-6 kg
F1 = 5 N , 30° above + X axis
F2 = 7.2 N, 45° above - X axis
F3 = 3.8 N, 22° below + X axis
let F be the net force which makes an angle θ from + X axis.
Now resolve the components of forces along X axis and y axis, we get
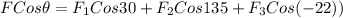
FCosθ = 5 Cos30° + 7.2 Cos 135° + 3.8 Cos22°
F Cosθ = 4.33 - 5.09 + 3.52
F Cosθ = 2.76 N .... (1)
Similarly,

F Sinθ = 5 Sin30° + 7.2 Sin 135° - 3.8 Sin22°
F Sinθ = 2.5 + 5.09 -1.42
F Sinθ = 6.17 N .... (2)
Squaring both the equations and then add, we get
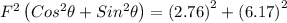
F = 6.76 N
Dividing equation (2) by equation (1), we get
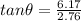
θ = 65.9°
Now,
Force = mass x acceleration
F = ma