Answer:
The general solution of the ODE is
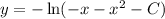 .
.
Explanation:
The given differential equation is

We need to find the general solution of the given ODE.
Use variable separable method to solve the above equation.
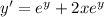
It can be written as
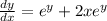
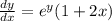
Separate the variables.
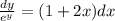
Integrate both sides.
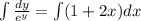
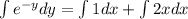
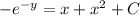
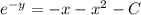
Taking ln both sides.

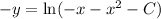
![[\because \ln e^x=x]](https://img.qammunity.org/2020/formulas/mathematics/college/mu4sbl88qi2np9eo0yf57s4uubi6hqgag5.png)
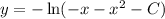
Therefore the general solution of the ODE is
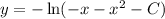 .
.