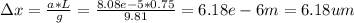Question

Mountain pull. A large mountain can slightly affect the direction of ""down"" as determined by a plumb line. Assume that we can model a mountain as a sphere of radius R = 1.00 km and density (mass per unit volume) 2.6 × 103 kg/m3. Assume also that we hang a 0.750m plumb line at a distance of 3R from the sphere's center and such that the sphere pulls horizontally on the lower end. How far would the lower end move toward the sphere?

Answer 1

6.18 um

Step-by-step explanation:

The plumb line will be pulled down by a combination of the gravitationall pull of Earth and of the mountain. The Earth pulls down and the mountain to the side. Because of this it will fall not in a straight line down, but slightly to the side. Since the plumb line will follow the compound gravity we can imagine a rectangle triangle formed by the plumb line, a vertical line that ends at the same height as the plumb line, and the sideways displacement.

The total gravity will be proportional to the plumb line lenght, the vertical line will be proportional to Earth's gravity and the sideways displacement to the mountain pull.

The gravity of Earth is 9.81 m/s^2

The pull of the mountain will be defined by Newton's law of universal gravitation:

`F = G (m1 * m2)/(r^2)`

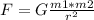
Where

F: pull force

G: universal gravitational constant (6.67e-11 m^3/(kg * s)

m1: mass of the mountain

m2: mass of the plumb

r: distance between mountain and plumb (3 km in this case)

If we divide both sides by m2 we obtain the acceleration towards the mountain of the plumb

`a = G (m1)/(r^2)`

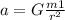
Now we need the mass of the mountain. This will be its volume times it's density. The volume depends on the radius (since we consider it as a sphere)

`m1 = \delta * (4)/(3) * \pi * r^3`

`m1 = 2.6e3 * (4)/(3) * \pi * 1000^3 = 1.09e13 kg`

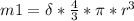
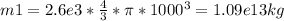
So, the acceleration on the plumb will be

`a = 6.67e-11 (1.09e13)/(3000^2) = 8.08e-5 m/s^2`

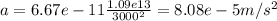
This is very small compared to the pull of Earth, so we can make an approximation that the length of the plumb line is equal to vertical line.

We can use the principle of similar triangles to say that:

`(\Delta x)/(L) = (a)/(g)`

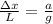
So:

`\Delta x = (a * L)/(g) = (8.08e-5 * 0.75)/(9.81) = 6.18e-6 m = 6.18 um`