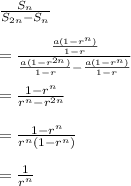Proof with explanation:
We know that the sum of first 'n' terms of a Geometric progression is given by
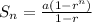
where
a = first term of G.P
r is the common ratio
'n' is the number of terms
Thus the sum of 'n' terms is
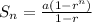
Now the sum of first '2n' terms is
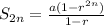
Now the sum of terms from
 to
to
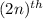 term is
term is

Thus the ratio becomes