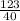Answer:
see explanation
Explanation:
Given the 3 equations
3x + 5y + 5z = 1 → (1)
x - 2y = 5 → (2)
2x + 4y = 11 → (3)
Use (2) and (3) to solve for x and y
Multiply (2) by 2
2x - 4y = 10 → (4)
Add (3) and (4) term by term
4x = 21 ( divide both sides by 4 )
x =
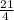
Substitute this value of x into (3)
2 ×
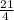 + 4y = 11
+ 4y = 11
 + 4y = 11 ( subtract
+ 4y = 11 ( subtract
 from both sides )
from both sides )
4y =
 ( divide both sides by 4 )
( divide both sides by 4 )
y =
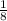
Substitute the values of x and y into (1) and solve for z
3 ×
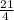 + 5 ×
+ 5 ×
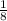 + 5z = 1
+ 5z = 1
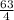 +
+
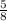 + 5z = 1
+ 5z = 1
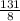 + 5z = 1 ( subtract
+ 5z = 1 ( subtract
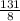 from both sides )
from both sides )
5z = -
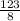 ( divide both sides by 5 )
( divide both sides by 5 )
z = -
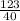
Solution is
x =
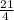 , y =
, y =
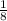 , z = -
, z = -