Question

Which of the following is a solution to...


Please answer asap

Answer 1

Start with

`4|x+3|\geq 8`

Divide both sides by 4:

`|x+3|\geq 2`

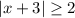
Now we "solve" the absolute value. It depends on the sign of its argument, so we have:

CASE 1: x+3>0

In this case, i.e. if x>-3, the argument of the absolute value is positive, and so it remains unchanged. The equation becomes

`x+3\geq 2 \iff x \geq -1`

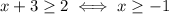
We can accept this solution, because it is compatible with the request x>-3.

CASE 2: x+3<0

In this case, i.e. if x<-3, the argument of the absolute value is negative, and so its sign is inverted. The equation becomes

`-x-3\geq 2 \iff -x \geq 5 \iff x \leq -5`

We can accept this solution, because it is compatible with the request x<-3.

Answer 2

C.
`x\le -5 \text{ or }\ x\ge -1`

Explanation:

Consider inequality
`4|x+3|\ge 8`

Divide it by 4:

`|x+3|\ge 2`

This inequality is equivalent to two inequalities:

`\left\[\begin{array}{l}x+3\ge 2\\x+3\le -2\end{array}\right.`

Hence

`\left\[\begin{array}{l}x\ge -1\\x\le -5\end{array}\right.`

So,

`x\le -5 \text{ or }\ x\ge -1`