Answers:
a)
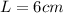
b)
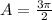
Explanation:
a) The area of the sector of a circle
 is given by:
is given by:
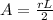 (1)
(1)
and
 (2)
(2)
Where:
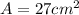
 is the radius
is the radius
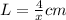 (3) is the length of arc
(3) is the length of arc
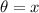 is the angle in radians
is the angle in radians
In this case we have to find the value of
 . So, let's begin substituting the known values in (1):
. So, let's begin substituting the known values in (1):
 (4)
(4)
Isolating
 :
:
 (5)
(5)
Substituting (5) in (3):
 (6)
(6)
Solving:
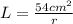 (7) At this point we have
(7) At this point we have
 , but we need to find the value of
, but we need to find the value of
 in order to have the actual value of the length of arc.
in order to have the actual value of the length of arc.
Making (1)=(2):
 (8)
(8)
Isolating
 :
:
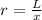 (9)
(9)
Substituting (7) and (5) in (9):
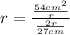 (10)
(10)
Finding
 :
:
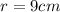 (10) Now that we have the value of the radius, we can substitute it in (7) and finally find the value of the
(10) Now that we have the value of the radius, we can substitute it in (7) and finally find the value of the

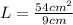 (11)
(11)
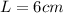 (12)
(12)
b) In this second case we have:
 is the length of arc
is the length of arc
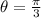 is the angle in radians
is the angle in radians
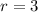 the radius
the radius
We have to find the area of the sector
 and we will use equations (1) and (2):
and we will use equations (1) and (2):
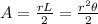 (13)
(13)
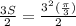 (14)
(14)
 (15)
(15)
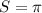 (16)
(16)
Knowing
 :
:
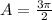 This is the area of the sector of the circumference.
This is the area of the sector of the circumference.