Question

A 5 cm diameter iron ball at 80°C is dropped into an insulated tank that contains 0.5 m^3 of liquid water at 25°C. Determine the temperature when thermal equilibrium is reached.

Answer 1

T= 25.0061 °C

Step-by-step explanation:

Given that

For iron ball:

d=5 cm

We know that for iron

`C_p=0.46\ (KJ)/(Kg-K)`

`\rho =7870\ (Kg)/(m^3)`

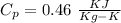
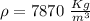
So the mass of iron

`m=\rho (4)/(3)\pi r^3`

Now by putting the values

`m=7870* (4)/(3)\pi * 0.025^3`

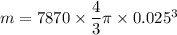
m=0.51 kg

Foe water:

`C_p=4.187\ (KJ)/(Kg-K)`

`\rho =1000\ (Kg)/(m^3)`

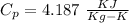
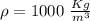
m=1000 x 0.5 kg

m=500 kg

So

heat loss by iron ball = heat gain by water

`\left (mC_p\Delta T\right )_(iron)=\left (mC_p\Delta T\right )_(water)`

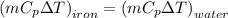
Lets take T is the final temperature

0.51 x 0.46 (80 -T) = 500 x 4.187 x (T-25)

T= 25.0061 °C