Question

RS has an endpoint at R(6,- 4) and length 17. Which of the following cannot be the coordinates of S?

Choose the correct answer below.
OA (-9,- 12)
O B. (23,-4)
OC. (6,13)
OD. (14.11)
O E. (23.13)

Answer 1

Option E (23,13)

Explanation:

we know that

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

Verify each case

case A) (-9,-12)

Determine the distance and then compare with the given length of 17 units

R(6,-4)

`d=\sqrt{(-4+12)^(2)+(6+9)^(2)}`

`d=√(289)`

`d=17\ units`

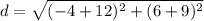
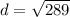
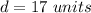
therefore

The given point can be the coordinates of S because the length RS is 17 units

case B) (23,-4)

Determine the distance and then compare with the given length of 17 units

R(6,-4)

`d=\sqrt{(-4+4)^(2)+(6-23)^(2)}`

`d=√(289)`

`d=17\ units`

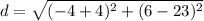
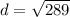
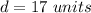
therefore

The given point can be the coordinates of S because the length RS is 17 units

case C) (6,13)

Determine the distance and then compare with the given length of 17 units

R(6,-4)

`d=\sqrt{(-4-13)^(2)+(6-6)^(2)}`

`d=√(289)`

`d=17\ units`

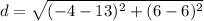
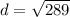
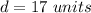
therefore

The given point can be the coordinates of S because the length RS is 17 units

case D) (14,11)

Determine the distance and then compare with the given length of 17 units

R(6,-4)

`d=\sqrt{(-4-11)^(2)+(6-14)^(2)}`

`d=√(289)`

`d=17\ units`

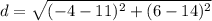
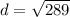
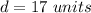
therefore

The given point can be the coordinates of S because the length RS is 17 units

case E) (23,13)

Determine the distance and then compare with the given length of 17 units

R(6,-4)

`d=\sqrt{(-4-13)^(2)+(6-23)^(2)}`

`d=√(578)`

`d=24.04\ units`

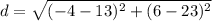
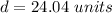
therefore

The given point cannot be the coordinates of S because the length RS is not 17 units