Answer:
The fourth point of the parallelogram is one point among (-2,2), (2,10) and (8,-12).
Explanation:
Given information: The first three vertices of parallelogram are (0,6), (5, -1) and (3,-5).
Let fourth point of the parallelogram is (a,b).
Diagonals of a parallelogram bisect each other. It means midpoint of both diagonals are same.
Midpoint formula:
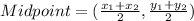
Case 1: If the point (0,6), (5, -1) and (3,-5) are consecutive, then pairs of opposite vertices are (0,6) and (3,-5), (5,-1) and (a,b).
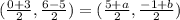
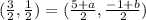
On comparing both sides, we get

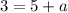
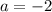
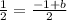
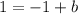
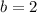
It means the fourth point of the parallelogram is (-2,2).
Case 2: If the point (0,6), (5, -1) and (3,-5) are not consecutive, then pairs of opposite vertices are (0,6) and (5,-1), (3,-5) and (a,b).
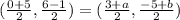
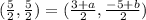
On comparing both sides, we get
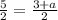
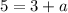
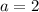
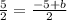
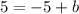
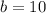
It means the fourth point of the parallelogram is (2,10).
Case 3: If the point (0,6), (5, -1) and (3,-5) are not consecutive, then pairs of opposite vertices are (5,-1) and (3,-5), (0,6) and (a,b).
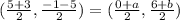
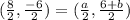
On comparing both sides, we get
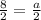
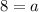
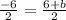
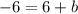
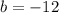
It means the fourth point of the parallelogram is (8,-12).