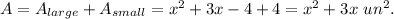Question

Express the area of the plane figure shown as a polynomial in standard form.

Answer 1

`A=x^2+3x\ un^2.`

Explanation:

The figure consists of two rectangles.

The larger rectangle has the length of (x+4) units and the width of (x-1) units.

The smaller rectangle has the width of (x-(x-1))=(x-x+1)=1 unit and the length of ((x+4)-x)=(x+4-x)=4 units.

The area of the rectangle is

`A_(rectangle)=\text{width}\cdot \text{length}`

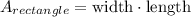
Calculate the area of each rectangle:

`A_(large)=(x-1)(x+4)=x^2 +4x-x-4=x^2 +3x-4\ un^2 .\\ \\A_(small)=1\cdot 4=4\ un^2.`

So, the area of the whole figure is

`A=A_(large)+A_(small)=x^2+3x-4+4=x^2+3x\ un^2.`