Question

A pump is put into service at the coast where the barometric pressure is 760 mm Hg. The conditions of service are : Flow rate 0,08 m2/s, suction lift 3,5 metres, suction pipe friction loss 0,9 metres, water temperature 65°C, water velocity 4 m/s. Under these conditions of service, the pump requires an NPSH of 2,1 metres. Assuming the density of water as 980,6 kg/m3, establish whether it will operate satisfactorily.

Answer 1

Yes, the Pump will operate satisfactorily, because the NPSH is greater than required.

Step-by-step explanation:

NPSH isa measure of how likely the fluid at the suction end of the pump is to experience cavitation. We always need NPSH to be above a given treshold required by the pump.

The definition of NPSH is:

`NPSH= (P_(atm)-P_(v))/(\rho \, g)-h-h_f`

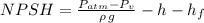
Where:

• 
  `P_(atm)` and
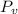  `P_(v)` are atmospheric and vapour pressure correspondingly.
• 
  `h` is suction lift and
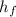  `h_f` is friction loss in meters.
• 
  `\rho` is the fluid's density
• 
  `g` is gravity, at sea level taken as
  `9.81 \, m/s^2`

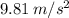
Extra Data: Water's vapour pressure at 65°C

`P_v =25.022 \, kPa`

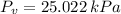
We can now calculate the NPSH

`NPSH= (101325-25022)/(980.6*9.81)\, m-3.5\, m- 0.9 \, m\\NPSH= 7.932\, m-3.5\, m- 0.9 \, m\\NPSH=3.532 \, m`

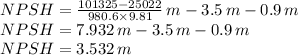
We can see that our NPSH is greater than the required NPSH:
`NPSH>NPSH_(req) = 2.1 \, m`

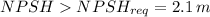
Thus our pump will operate without cavitation.