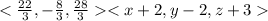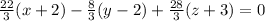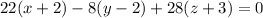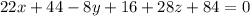Question

Find an equation of the plane. The plane that passes through the point (−2, 2, 3) and contains the line of intersection of the planes x + y − z = 2 and 2x − y + 3z = 2

Answer 1

`22x-8y+28z=-144`

Explanation:

Equations of lines,

x + y - z = 2,

2x - y + 3z = 2

If z = 0,

Equations would be,

x + y = 2

2x - y = 2

Adding these equations, we get, 3x = 4 ⇒ x =
`(4)/(3)`

`\implies (4)/(3) + y = 2\implies y = 2 - (4)/(3) = (6-4)/(3) = (2)/(3)`

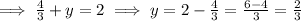
Thus, solution would be ( 4/3, 2/3, 0)

Now, if x = 0,

Equation are,

y - z = 2,

-y + 3z = 2

Adding equations, We get, 2z = 4 ⇒ z = 2,

⇒ y - 2 = 2 ⇒ y = 2 + 2 = 4,

Thus, solution would be ( 0, 4, 2 )

Let a be the vector from (-2, 2, 3) to (4/3, 2/3, 0)

⇒ a = (4/3 + 2)i + (2/3 -2)j + (0-3)k =
`(10)/(3)i-(4)/(3)j-3k`

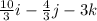
Similarly,

Let b be the vector from (-2, 2, 3) to (0, 4, 2),

⇒ b = (0+2)i + (4-2)j + (2-3)k ⇒ b = 2i + 2j - k

So, the normal of the plane is,

`n=a* b = \begin{vmatrix}i & j & k \\ (10)/(3) & -(4)/(3) & -3 \\ 2 & 2 & -1\end{vmatrix}=(22)/(3)i-(8)/(3)j+(28)/(3)k`

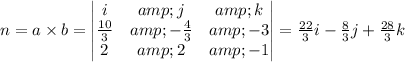
∵ General equation of a plane,

`n.<x-x_0, y-y_0, z-z_0>=0`

Hence, the equation of the given plane is,

`<(22)/(3), -(8)/(3), (28)/(3)><x+2, y-2, z+3>`

`(22)/(3)(x+2) -(8)/(3)(y-2)+(28)/(3)(z+3)=0`

`22(x+2)-8(y-2)+28(z+3)=0`

`22x+44-8y+16+28z+84=0`

`\implies 22x-8y+28z=-144`