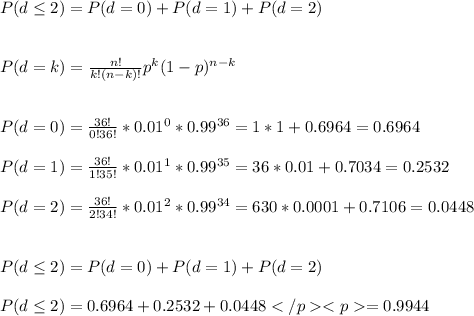Answer:
The probability of accepting this shipment is 0.9944.
The company will accept 99.44% of the shipments and reject 0.66% of the shipments.
Explanation:
The shipment will be accepted if at most 2 batteries do noy meet the specifications in the sample of 36 batteries.
We can model this as a binomial distribution, with sample size of n=36 and probability of defective of p=0.01.
The probability of having at most 2 batteries defective is: