Question

If, in a single-period inventory situation, the probabilities of demand being 1, 2, 3, or 4 units are .3, .3, .2, and .2, respectively. If two units are stocked, what is the probability of selling both of them?

Answer 1

The probability of selling two units is 0.7.

Explanation:

It is given that in a single-period inventory situation, the probabilities of demand being 1, 2, 3, or 4 units are 0.3, 0.3, 0.2, and 0.2, respectively.

It means,

`P(1)=0.3`

`P(2)=0.3`

`P(3)=0.2`

`P(4)=0.2`

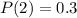
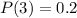
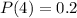
If two units are stocked, both of them are sold. It means the demand must be 2 or greater than 2.

The probability of selling two units is

`P=P(2)+P(3)+P(4)`

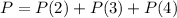
Substitute the given probabilities in the above formula.

`P=0.3+0.2+0.2`

`P=0.7`

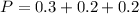
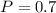
Therefore the probability of selling both of them is 0.7.