Answer:
(a) 0.8 s
(b) t = 7.2 s
Step-by-step explanation:
(a) Half life expression for second order kinetic is:
![t_(1/2)=(1)/(k[A_o])](https://img.qammunity.org/2020/formulas/chemistry/college/dtbcugt1e5y67l6hck0xrmf78wr0xtmewi.png)
Where,
![[A_o]](https://img.qammunity.org/2020/formulas/chemistry/high-school/38eb24kf04xqy5t88y9g0vzh3m04r4nqgg.png) is the initial concentration = 1.0 M
is the initial concentration = 1.0 M
k is the rate constant = 1.25 M⁻¹s⁻¹
So,
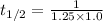
Half life = 0.8 s
(b) Integrated rate law for second order kinetic is:
![(1)/([A_t]) = (1)/([A]_0)+kt](https://img.qammunity.org/2020/formulas/chemistry/college/vnlj8ajczxopxxojfk73ilai64ieoyqgnm.png)
Where,
![[A_t]](https://img.qammunity.org/2020/formulas/chemistry/college/wbj92t0z4axifcyqa24z3ary269op2iva8.png) is the final initial concentration
is the final initial concentration
For 90% completion, 10% is left. so,
![[A_t]=\frac {10}{100}* 1.0=0.1\ M](https://img.qammunity.org/2020/formulas/chemistry/college/cfizg7dvqavscb9r730sxkh6hbcx7rsbrk.png)
So,
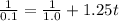
t = 7.2 s