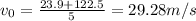Answer:
The answer is 29.28 m/s
Step-by-step explanation:
This is a classic exercise of projectile motion. If the ball is thrown straight up, then the movement is in one dimension, the y axis, and the equation you need is
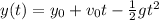
where
 is the height at a time "t",
is the height at a time "t",
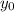 is the initial position,
is the initial position,
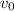 is the initial velocity and "g" is the acceleration of gravity.
is the initial velocity and "g" is the acceleration of gravity.
If you wonder where this equation came from, you just need to draw the force diagram applied to the ball. Considering that the only force that affects the trajectory of the ball is its weight,
total force = -mg = ma
where "m" and "a" are the mass of the ball and its acceleration respectively, and the negative sign is due to the direction of gravity (straight down). From this equation we get that a = -g, but acceleration is the variation of velocity, then
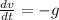
solving the differential equation, we get
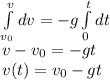
Once again, velocity is the variation of position, so

then
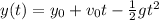 .
.
Now, getting back to the problem,
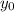 = 0, and
= 0, and
 = 23.9 m at t = 5 s. So
= 23.9 m at t = 5 s. So
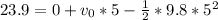 , then
, then