Question

The probability of a potential employee passing a training course is 86%. If you selected 15 potential employees and gave them the training course, what is the probability that more than "11" will pass the test?

Answer 1

Answer: 0.9526

Explanation:

Binomial probability formula to find the probability of getting success in x trial :-

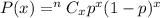`P(x)=^nC_xp^x(1-p)^x`, where p is the probability of success and n is the sample size .

Given : The probability of a potential employee passing a training course is 86%.

i.e. p=0.86

Sample size : n=15

Then, the probability that more than "11" will pass the test:-

`P(x\geq11)=P(11)+P(12)+P(13)+P(14)+P(15)\\\\=^(15)C_(11)(0.86)^(11)(0.14)^(4)+^(15)C_(12)(0.86)^(12)(0.14)^(3)+^(15)C_(13)(0.86)^(13)(0.14)^(2)+^(15)C_(14)(0.86)^(14)(0.14)^(1)+^(15)C_(15)(0.86)^(15)(0.14)^(0)\\\\=(15!)/(11!4!)(0.86)^(11)(0.14)^(4)+(15!)/(12!3!)(0.86)^(12)(0.14)^(3)+(15!)/(13!2!)(0.86)^(13)(0.14)^(2)+(15)(0.86)^(14)(0.14)^(1)+(1)(0.86)^(15)(0.14)^(0)\\\\=0.952154074749\approx0.9526`

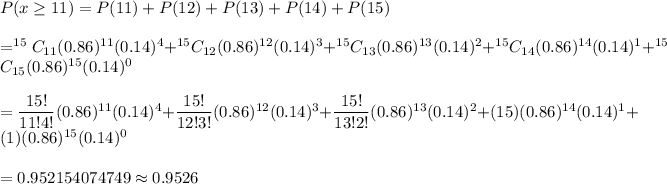
Hence, the probability that more than "11" will pass the test =0.9526