Data:
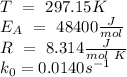
Step-by-step explanation:
The rate constant as a function of the temperature can be expressed using the Arrhenius equation, as follows,
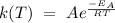
Then, find a value for the constant A, according to the data given in the exercise,


As the rate constant has units
![[s^(-1)]](https://img.qammunity.org/2020/formulas/chemistry/college/8twvd5i7yvj4snz7s741vu6f4pzsiyeppj.png) then, the reaction corresponds to one of first order. Then, the reaction corresponds to:
then, the reaction corresponds to one of first order. Then, the reaction corresponds to:
![r \ = \ k(T) \ [A]](https://img.qammunity.org/2020/formulas/chemistry/college/5ce4b0jtgeap0drc7mh332g9jh80z2y303.png)
Which tell the amount of mass (mol) is produced by second per unity of volume.
Answer:
If the reaction goes twice fast, the reaction rate corresponds to,
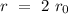
The expression above can be reduced to:
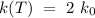
Replacing k(T) in order to obtain the temperature T,
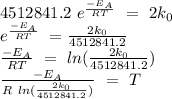
Replacing all values,
